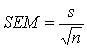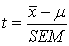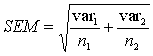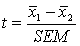How to do simple t-tests
These are statistical tests that will tell you if there is a significant difference between two sets of data, or if the average of a set of data differs significantly from a predicted value.
The results of these tests are only valid when the data are normally-distributed. If the data are not normally-distributed, use another statistical test, such as the Mann-Whitney U-test.
Explanation of terms
n = The sample size
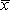 = The mean of a sample = The mean of a sample
µ = The theoretical mean of a population
s = The standard deviation
var = The variance (equal to s²)
The standard deviation (s) can be calculated using the formula:

Or in Microsoft Excel (where A1:A10 is the range of cells containing the data):
=STDEV(A1:A10)
|
One-sample t-test
To test whether the mean of a sample (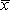 ) differs significantly from a predicted value (µ)...
) differs significantly from a predicted value (µ)...
Calculate the 'standard error of the mean' (SEM):
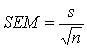
Calculate the t-statistic:
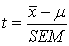
Use the table of critical values (below) to find out whether or not the result is significant.
Two-sample t-test
To test whether the mean of a sample (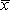 1) differs significantly from the mean of another sample (
1) differs significantly from the mean of another sample (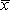 2)...
2)...
Calculate the 'standard error of the mean' (SEM):
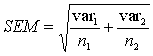
Calculate the t-statistic:
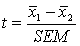
Use the table of critical values (below) to find out whether or not the result is significant.
Alternatively, type the following formula into Microsoft Excel (where A1:A10 and B1:B10 are the ranges of cells containing the data):
=TTEST(A1:A10,B1:B10,2,3)
This will give you a p-value (see below) indicating how significant the result is.
Table of critical values
The table below gives the t-value at which the result has a particular level of 'significance'.
d.f. is the number of 'degrees of freedom'. In this case, d.f. = n -1
(If the exact d.f. value that you want is not included in the table, use the closest value below it that is included.)
p is the probability that the difference between two samples, or the difference between a sample and the theoretical result, is entirely due to chance.
| d.f. |
p=0.1 |
p=0.05 |
p=0.01 |
| 2 |
2.92 |
4.30 |
9.92 |
| 3 |
2.35 |
3.18 |
5.84 |
| 4 |
2.13 |
2.78 |
4.60 |
| 5 |
2.02 |
2.57 |
4.03 |
| 6 |
1.94 |
2.45 |
3.71 |
| 7 |
1.89 |
2.36 |
3.50 |
| 8 |
1.86 |
2.31 |
3.36 |
| 9 |
1.83 |
2.26 |
3.25 |
| 10 |
1.81 |
2.23 |
3.17 |
| 11 |
1.80 |
2.20 |
3.11 |
| 12 |
1.78 |
2.18 |
3.05 |
| 13 |
1.77 |
2.16 |
3.01 |
| 14 |
1.76 |
2.14 |
2.98 |
| 15 |
1.75 |
2.13 |
2.95 |
| 16 |
1.75 |
2.12 |
2.92 |
| 17 |
1.74 |
2.11 |
2.90 |
| 18 |
1.73 |
2.10 |
2.88 |
| 19 |
1.73 |
2.09 |
2.86 |
| 20 |
1.72 |
2.09 |
2.85 |
| 21 |
1.72 |
2.08 |
2.83 |
| 22 |
1.72 |
2.07 |
2.82 |
| 23 |
1.71 |
2.07 |
2.81 |
| 24 |
1.71 |
2.06 |
2.80 |
| 25 |
1.71 |
2.06 |
2.79 |
| 26 |
1.71 |
2.06 |
2.78 |
| 27 |
1.70 |
2.05 |
2.77 |
| 28 |
1.70 |
2.05 |
2.76 |
| 29 |
1.70 |
2.05 |
2.76 |
| 30 |
1.70 |
2.04 |
2.75 |
| 35 |
1.69 |
2.03 |
2.72 |
| 40 |
1.68 |
2.02 |
2.70 |
| 45 |
1.68 |
2.01 |
2.69 |
| 50 |
1.68 |
2.01 |
2.68 |
| 60 |
1.67 |
2.00 |
2.66 |
| 70 |
1.67 |
1.99 |
2.65 |
| 80 |
1.66 |
1.99 |
2.64 |
| 90 |
1.66 |
1.99 |
2.63 |
| 100 |
1.66 |
1.98 |
2.63 |
| Infinity |
1.64 |
1.96 |
2.58 |
Example: suppose that a t-test on a sample of 10 individuals (d.f. = 9) produced a t-value of 3.0. The table tells us that p is between 0.01 and 0.05 in this case (p=0.05 when t=2.26, and p=0.01 when t=3.25; our t-value lies in between these two). Therefore, the probability of the result arising by chance is less than 5% (p<0.05), so this is a fairly significant result.
More teachers' notes
© Andrew Gray, 2006
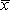 = The mean of a sample
= The mean of a sample